HollowGram Wheels D.R.A.F.T Technology D.R.A.F.T Technology D.R.A.F.T Technology

D.R.A.F.T. and HollowGram Wheels

空力性能は、ホログラムホイールのキーです。R-64シリーズは、リムハイトが高くハイスピードをもたらし、風を切り裂き、どこまでも走り続けることをサポートします。R-50シリーズは、R-64の空力性能をそのままに、より軽く、オールラウンドなレース用ホイールです。R45は、エアロダイナミクスの技術を低価格で提供し、ライダーがこれまで以上に簡単にRise to Speedできるようにします。

ロードホイールのエアロダイナミクスは複雑で、さまざまな流体力学の原理やニュアンスを理解する必要があります。キャノンデールはD.R.A.F.T.（Drag Reducing Aerodynamic Flow Technology）という考え方に基づき、すべてのホログラムホイールを開発しています。D.R.A.F.T.という空力設計へのアプローチにより、実際のライド下で最適な空力性能を発揮します。ヨー角による空気抵抗の変化と実データを組み合わせることで、ホログラムホイールがあらゆる走行状態で最高のパフォーマンスを発揮することを保証しています。

リムとタイヤ

ロード用ホイールのR-64、50、45は、最も一般的なロードタイヤサイズで最高のパフォーマンスを発揮するように、内幅21mm、外幅32mmを採用しています。タイヤはホイールのエアロダイナミクスにかかわる非常に重要な要素です。特に前輪のタイヤは、自転車のなかで最初に空気に触れる部分なので、タイヤとリムの相互作用によって後方へ流れる空気が乱気流となり、大きな抵抗を生み出すことになります。空気力学的に見ると、自転車のタイヤは一般的には効率の良い形状ではないため、リムはタイヤと協力し合い、空気抵抗を最小限に抑える必要があります。空気抵抗を抑えるためには、タイヤによって一度乱れた空気が、なるべくリム側面を沿うように後方へ流れきることが重要です。考え抜かれたリム幅とその形状により、ホログラムホイールはタイヤの構造やサイズの影響を受けにくく、ワイドタイヤを使用した場合は空気抵抗を最小限に抑えることができます。

D.R.A.F.Tとは？

D.R.A.F.T.は、HollowGramの包括的な空力開発哲学に付けられた名前です。その中核となるのが「Yaw Weighted Drag」と呼ばれるヨー角による抵抗差を意味し、実世界のオンロードライドにおける風条件下で、空力性能を評価するための自社開発・査読済みのプロセスです。あらゆる角度から受ける風の抵抗下で、ライダーのスピードを最大化するための最適な設計を実現しています。

ヨーウェイトドラッグとは何か、なぜ重要なのか？

製品の開発・テストでは、さまざまなヨー角（進行方向と有効風向のなす角）で抵抗を評価します。図1（下）は、ヨー角に対する抗力をプロットしたものです。これは、風洞実験による典型的な出力です。. ヨー角の関数として抗力が大きく変化していることに注目してください このプロットでは、車輪の抗力はヨー角が大きくなるにつれて減少し、変曲点では急激に増加することがわかります。この挙動は、高性能なホイールによくあるものです。

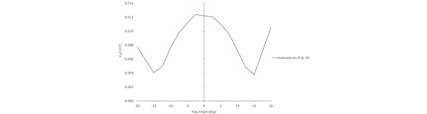
ヨー角により空気抵抗が変化するため、外での性能を評価するためにどのヨー角を使うべきかという疑問が浮かびます。これは、曲線が交差する2つの構成を比較する場合に、特に重要です。(例：下の図2)

例えば、同じタイヤでテストしたキャノンデールホログラムR-SL 50とスペシャライズドロバールラピッドCLXを比較してみましょう。この場合、どちらのホイールも、ヨーのスペクトルの異なるポイントで最も抵抗が小さいと主張することができます。

どのヨー角が一番重要なのか？

ライダーが受けるヨー角が均等であれば、これらの結果を単純に数値で平均することで、適切な平均抗力数値が得られるでしょう。しかし、実際にはヨー角は均等に分布しないので、この影響を考慮する必要があります。

ヨー角と風角は同じではないことに留意してください ライダーが動いているときは、前方へ動こうとする気流があり、これが大気と組み合わさり、結果としてヨー角が生まれます。ですので、ヨー角は風速、風向、路面速度の関数です。風速と風向の統計関数と、前進運動の幾何学的効果を組み合わせて、ヨー角分布の解析モデルを決定しています。その結果、ヨー角0度を中心としたベルカーブになります（下図3参照）。

この重み付け関数を用いて、風洞実験の結果を変換し、ライダーが道路上でそのヨー角を見る確率に比例して抗力の大きさがスケールされるプロットを作成します。ヨーウェイトドラッグは、ウェイトドラッグプロットの加重平均を取ることで算出されます。

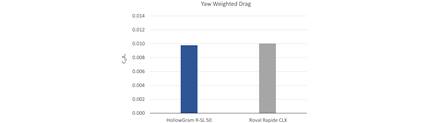
ヨーウェイト抗力という観点から見ると、この2つのホイールの空力性能はほとんど差がないことがわかります。この方法は、分析に2つの明確な利点があります。まず、大きなデータのサブセットを、ヨー角の関数としての抗力と、道路上でのヨー角の可能性の両方を包含する、各構成の単一の値にまとめることによって、分析プロセスを簡素化します。第二に、風洞実験の結果を鵜呑みにすることなく、路上での性能を客観的に比較することができることです。

ライダーが経験するさまざまなライディングコンディションにおいて完全に最適化されるように、すべてのパフォーマンス製品を開発する際にヨーウェイトドラッグを使用しています。

ヨーウェイト抵抗の導出の詳細については、こちらの論文をお読みください：

doi:10.3390/proceedings2060211

走行速度や風速は、このアプローチにどう影響するのでしょうか？

本事例では、走行速度40km/h、風速11km/hとしています。このモデルは硬直的なものではなく、さまざまな道路や風速に適用できるものです。路面速度を上げたり、風速を下げたりすると、ヨー分布がきつくなり、低ヨー角の強調が強まります。路面速度を下げたり、風速を上げたりするとヨー分布が平坦になり、低いヨー角の強調が減少します。時速40kmは、レースの平均的な速度であり、アマチュアが短時間で達成可能な速度であるため、時速40kmを使用しています。これは、高速道路の走行を見事に表現しています。平均風速の11km/hという値は、実験データから導き出されたもので、SAEがロードカーを評価する際の同様のアプローチと同じものです。